Enjoy DatePsychology? Consider subscribing at Patreon to support the project.
If you didn’t expect a statistics article on a psychology website that’s totally understandable. When I began my graduate program in psychology I did not expect that over half of my coursework would be in statistics. Even as a psychology undergraduate, where I tried to avoid math as much as I could, I was shocked to learn that I would be required to take three years of statistics for psychologists.
When you think about psychology it may call to mind clinical psychology, therapy and the diagnosis of clinical disorders, where the role of statistics is not immediately in the visible forefront. In research psychology, where the focus is almost entirely on conducting experiments following the scientific method, the role of statistics may be more clear. In both cases statistics is a foundation of the field. Statistics are used for hypothesis testing and applying evidence-based research to clinical practice.
If you have taken a statistics course one of the first concepts you will have learned is the sample. Essentially, taking (or sampling) a portion of a population in order to study that population. You can’t study the entire population, usually due to the size of any given population, or lack of access to the entire population, so you use a sample from that population.
How seemingly small samples represent large populations
We can make generalizations from seemingly small samples to huge populations. This fact is very counterintuitive for many people, yet it is a foundation of statistics.
Further, past a point, the utility of your sample size (as far as generalizability is concerned) begins to flatten. Increasing your sample size beyond that point may not help you very much. It probably won’t make your sample much more representative of the population it is taken from. (It could help more with sample power, or the ability to detect an effect, which I will describe in a section below.)
The central limit theorem, which gives us a normal distribution when random samples are taken from a population, allows us to generalize from samples to populations. The central limit theorem even allows us to quantify the degree of uncertainty, or in other words to know how closely our sample represents the general population.
For the central limit theorem to hold true we do need a sufficiently large sample. The key word is “sufficiently,” because “sufficiently large” may be much smaller than what you would expect. If you know that the population itself has a normal distribution, this can be as small as 10 subjects. If the population is not normally distributed the sample size begins at 30.
Thus 30 (n > 30) subjects is the general convention within statistics for the central limit theorem to hold.
If you have taken a statistics course the importance of sample size was one of the first things you will have learned, alongside sampling itself and the central limit theorem. It’s common for people to remember “big sample size,” or “how big should a sample be — as big as you can make it.” This is not wrong, but I have seen too many people interpret “big” as “big relative to the size of the population.” Large populations do not require proportionally large samples.
This does not mean that you should assume 30 people is a sufficient sample size, but rather that 30 is where we should begin to expect the central limit theorem to hold.
How do I know if the sample is big enough
You can’t know if a sample size is too small, or big enough, by feelings and intuition. You cannot look at a sample and intuitively know from the size of that sample alone if it is too small or too large.
You must have an idea of the size of the population your sample is taken from, as well as an idea of how closely you want your sample to reflect that population (represented as a percentage of confidence).
An equation exists for this, but commonly you will use a sample size calculator. I will use this sample size calculator for the examples below.
A sample large enough to generalize to the entire US population
How large of a sample do I need to generalize to the entire population of the United States — 330 million people in the following examples?
First, I need to determine my confidence level. This tells me the probability that the true value of the population falls within the estimate of my sample. This is usually set at 95% or 99%. The implication is that, running samples repeatedly, you would be wrong only 5% or 1% of the time.
Next I set my margin of error, which is an estimate of how far my sample may deviate from the true population. For example, if my margin of error is 5% and my sample predicts 100, I should expect a range between 95-105 (100∓5).
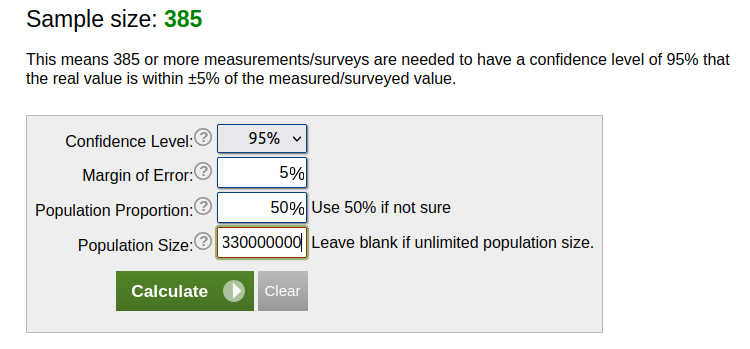
Using these values I can determine that I need a sample size of 385 people if I want to be able to generalize to the entire US population with a confidence level of 95% and a margin of error of 5%.
As this example shows, I might want more than 30 people. At the same time, a 385 person sample is only 0.000117% of the population. I do not need a sample that is large relative to the population.
What happens if I increase my sample size — does it help me much?
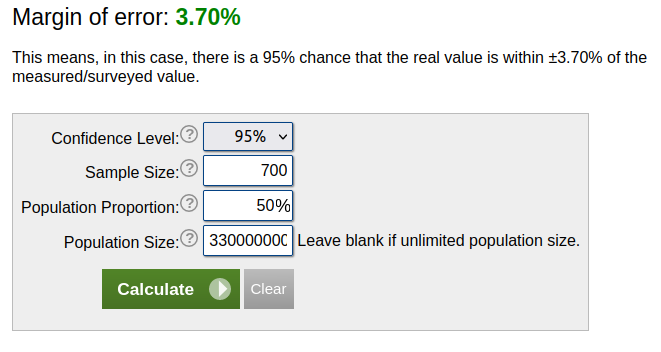
If I increase my sample size from 385 to 700, my margin of error only drops from 5% to 3.7%.
What happens if I reduce my sample size? By going from 385 to 175, my margin of error increases to 7.41%. By reducing it from 175 to 90, it goes from 7.41% to 10.33%. Again halving my sample size from 90 to 45 increases my margin of error to 14.16%. A sample size of 22 makes my margin of error leap up to 21%, while a sample size of 10 bumps it up to 31%.
If you can increase your sample size from 10 to 175, you reduce your margin of error by 24% and put it at a reasonable 7%. If you increase your sample size from 175 to 700, you only reduce your margin of error by about 4%.
As I said in the previous section, the larger your sample size becomes the more the representative benefit of a large sample size flattens. You get diminishing returns by increasing your sample size past a point. Visualized below:
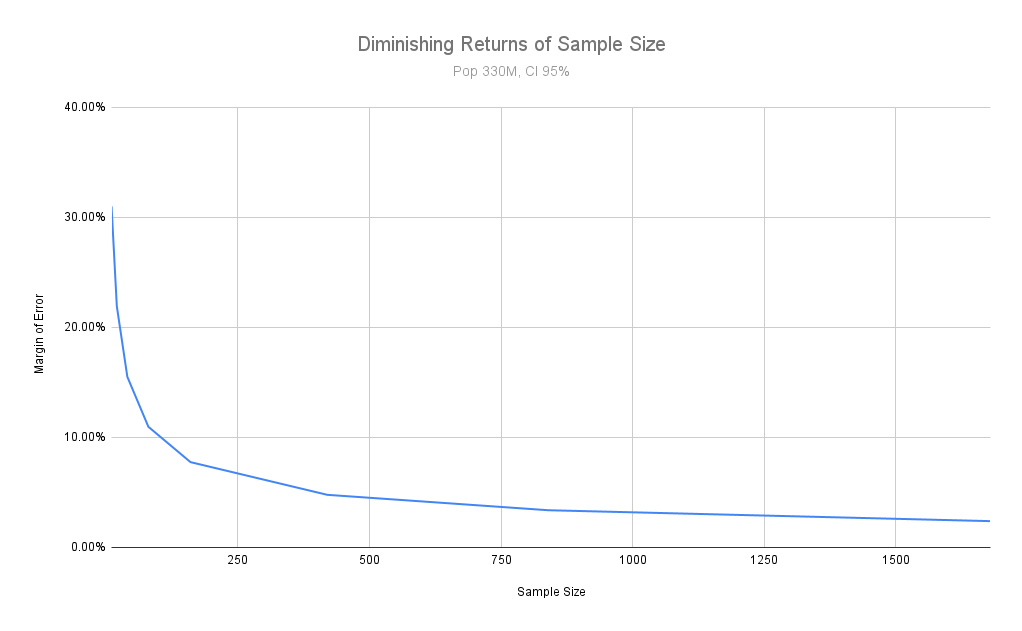
So how big should my sample size be? An industry convention in the field of nationally representative polls is 1000 people. Almost all nationally representative polls conducted by large polling firms in the US use sample sizes of 1000 people. This lets you set a confidence level higher at 99% as well.
When are sample sizes below 1000 good enough
What about the central limit theorem and the convention of 30 subjects as a starting point? If you are only able to get 30 people in your study, your margin of error is approximately 18%.
To use a hypothetical example, let’s say you collect data and find that the average man gets 15 matches on Tinder per month. 18% of 15 is 2.7, meaning that your estimate of 15 matches can be expected to be higher or lower by 2.7 matches.
A sample size of 80 would reduce your margin of error to 10%, or just 1.5 matches above or below 15.
Is this good enough? There is some subjectivity here, but it probably depends on what you are studying. A margin of error of 10% in the Tinder example still gives you a very reasonable estimate. If an estimate of 15 Tinder matches is off by 1.5 matches that is good enough for me, personally.
A 10% margin of error for an experimental drug could result in fatalities and be too high of a risk. It might not be good enough. Thus this depends on the field you are in and the consequences of missing your estimate.
Large populations do not require proportionally large samples
In the second section I wrote “large populations do not require proportionally large samples.” In the previous section we used the entire US population of 330 million people. If large populations do not require proportionally large samples, does this mean that smaller populations can get by on smaller samples? This depends on the population size.
Approximately 8 million Americans aged 18-30 are on the dating app Tinder. If I need 385 people for the US population of 330 million, does this mean I can get by with >50 people for a survey of Tinder users?
It might surprise you to see that you need the same sample size that you need for the entire US population: 385.
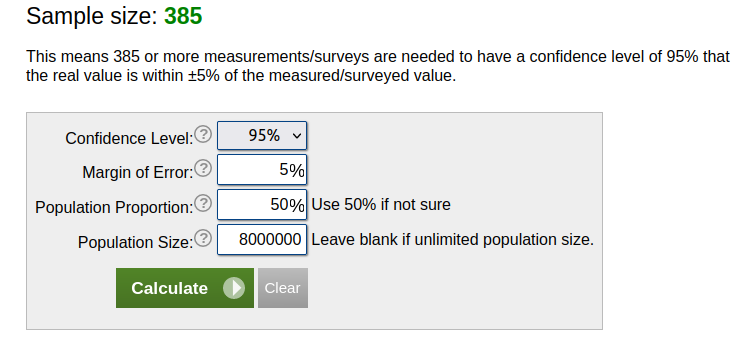
The simple explanation is that your population is still very large. You need a sufficiently large sample size to generalize to your population.
This illustrates two points. First, you probably can’t intuit a representative sample size. (An exception would be if you work with statistics and already have an idea of what sample sizes are needed for your population.) Second, large populations do not require proportionally large samples. You need the same sample size for a population of 8 million that you do for a population of 330 million.
Sampling methodology is more important than sample size for representativeness
In psychology (and across fields that use human subjects) we often don’t expect our samples to be fully generalizable to the general population to begin with. This is not due to sample size, but rather the heavy reliance on convenience samples in human research.
As mentioned in the second section, for the representativeness assumption to hold we need representative samples, which we achieve by random selection from a population. Every person in the population must have a chance of being selected.
When researching human beings in a messy world, this is often impossible or methodologically prohibitive. We take what we can get. A lot of the time this is college students in a classroom. Thus the expression in research: the best sample is the one that you have. If your sample is a WEIRD (White/Western, Educated, Industrialized, Rich, and Democratic) selection from the students in your class there are limitations to what assumptions you can make about the sample’s generalizability.
Being unable to quantify generalizability does not mean a sample is not generalizable
When we acknowledge the limitations of generalizability due to non-random selection we are saying we do not know, or that we can’t quantify, how generalizable our sample is. We can’t give it the randomness assumption of generalizability.
This is often misunderstood as saying the sample is not generalizable, or that it it is definitively unrepresentative.
In fact convenience samples may reflect a given population very well, depending on the nature of the sample.
For example, a WEIRD selection of young college students may reflect the behavior of young adults on Tinder very well. There is a good deal of overlap between young college students and Tinder users. Conversely, a WEIRD sample may not reflect the dating behavior of members of the indigenous Hadza in Tanzania.
Homogeneous convenience samples, or samples that are specifically limited to sociodemographic subpopulations, can have good generalizability to those populations (Jager et al., 2017).
This is good news for research on dating, relationships and attractiveness. As we draw many convenience samples from young college students in our own countries, we are often intentionally or unintentionally selecting from homogeneous subpopulations specifically relevant to our own lives. If you’re a young college student on Tinder, then a convenience sample of young college students may have great relevance (and generalizability) to the dating market that you are in.
The role of sample size in study power
The main purpose of most research is not to collect descriptive statistics about the population, as in a poll. The main purpose of research is hypothesis testing, which usually means some kind of comparison of groups.
For this we are very interested in sample size for power. Power here refers to our ability to determine an effect, or a difference between groups.
Let’s say I want to know if men in Idaho get more Tinder matches than men in New York. I need to know what sample sizes are required to determine if there is a difference between the two groups. Due to the nature of probabilistic statistical tests, if the size of my sample groups are very small I would need to see a very large difference between those groups to detect an effect. On the other hand, if my sample groups are very large then I am able to detect smaller differences between them.
This is all I am going to write about sample size and power for this article. It required a mention, but it is mostly a separate topic from sample size and representativeness.
Rejection of sample size as an excuse to dismiss research
When people claim that a sample size is too small they are almost never referring to the sample being underpowered, as in the previous section. They are usually making the claim that the sample is too small to make inferences about a population. As “large sample size” is the first thing anyone who has ever been exposed to statistics learns, it’s often the only criticism most people know how to make. And really, it’s mostly trotted out when people read the results of a study that challenges their beliefs. In this context it’s just an excuse to dismiss the results.
Hopefully with this article you now have the tools to determine if a sample really is too small, if a sample could be representative, and why or why not.
How to respond to the “small sample size” objection
- If someone tells you that a sample size is too small, ask them how big the sample needs to be and why. They probably won’t be able to give you an alternative sample size and justification for it (such as a lower margin of error).
- Ask them to present research with a different conclusion that supports their view. It’s not sufficient to point out methodological limitations in a paper. Finding a problem in someone else’s research is not empirical support for one’s own personal opinions.
- Determine if the objection is in good faith or if it is a motivated objection. If it is the latter, make peace with the fact you probably won’t change their mind no matter how much math you show them.
References
Jager, J., Putnick, D. L., & Bornstein, M. H. (2017). II. More than just convenient: The scientific merits of homogeneous convenience samples. Monographs of the Society for Research in Child Development, 82(2), 13-30.
Resources, if you want to know more about sample size and representativenss
How can a survey of 1,000 people tell you what the whole U.S. thinks?
Why a Large Sample Doesn’t Guarantee a Representative Sample
How to choose a sample size (for the statistically challenged)
Sample size in psychological research over the past 30 years
2 comments
Excellent article, Alexander! I want to thank you for clarifying the misconceptions around sample size in research. The unique aspect highlighted in your article is how the representativeness of a sample depends more on sampling methodology than on the absolute size of the population. You provided valuable insights into the fact that smaller populations do not necessarily require proportionally large samples. Moreover, your tips on responding to the “small sample size” objection are practical and helpful. Keep up the great work in debunking common misunderstandings in statistics and research!
Your suggestions 1-3 for how to respond miss the most important point. If your sample sizes are, in fact, low, then it is on *you* to make sure you know why it’s ok in your case. If you can’t give a cogent explanation of the contents of this very article and how your seemingly low sample size isn’t a problem, then there is likely an issue and you need to figure out whether your sample size is too small or not before asking anyone else to do your work for you. It is absolutely your responsibility to be able to explain why your sample size is appropriate and nobody else’s.